Home
A comprehensive resource for safe and responsible laser use
Laser dazzle and glare, a scientific definition
Dr. Craig Williamson and Dr. Leon McLin have done extensive studies of how laser light can block vision. Their work helps determine the parameters of visible-light laser interference with vision. There are two main parts:
Their work has applications in discussing various levels of dazzle that pilots might be exposed to.
It also has applications in defense and security. The concept makes it easier to determine how much laser light at what distance should be used for checkpoints, riot control and other situations where police or soldiers want to safely block an adversary’s vision.
- Determining how wide an area of vision can be blocked by dazzle, before a given task is difficult or impossible.
- Determining the laser power, color, divergence, distance and other parameters which will cause interfering vision blockage.
Their work has applications in discussing various levels of dazzle that pilots might be exposed to.
It also has applications in defense and security. The concept makes it easier to determine how much laser light at what distance should be used for checkpoints, riot control and other situations where police or soldiers want to safely block an adversary’s vision.
-
Background: How dazzle guidelines developed
- When laser illuminations of pilots first became an issue in the mid-1990s, safety experts needed to establish guidelines for “how much laser light is too much.” Specifically, they wanted to know how much laser light could cause afterimages, how much could cause veiling glare (you can’t see past the light), and how much could cause distraction.
Eventually these levels were set. But it was done somewhat by the seat of the pants. Some informal tests were done on volunteers in the SAE G10T Laser Safety Hazards Committee. After these tests, and some additional discussion and negotiation, three levels were set:- Afterimage: 100 microwatts/cm2. An exposure equal or greater than this would cause afterimages.
- Glare: 5 microwatts/cm2. An exposure between 100 µW/cm2 and 5 µW/cm2 would cause vision-blocking glare
- Distraction: 5 nanowatts/cm2. An exposure between 5 µW/cm2 and 5 nW/cm2 would not block vision but would be brighter than city and airport lights seen outside the cockpit window.
These levels became part of regulations used by the U.S. Federal Aviation Administration, and by other countries that base their regulations on SAE G10T and/or FAA.
However, many safety experts wanted more scientific validation of these levels. That is what Williamson and McLin worked on for many years in the mid-2010s. -
Background: Laser safety concepts MPE and NOHD
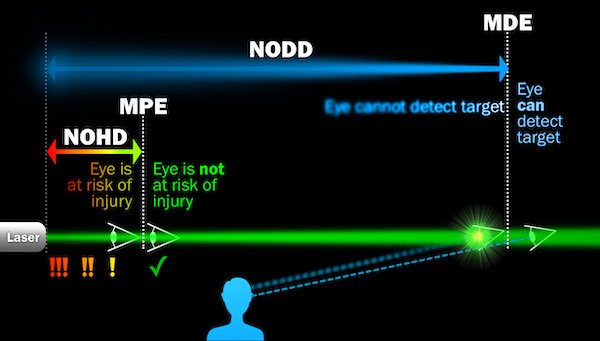
- In laser safety, two well-established concepts are the “Maximum Permissible Exposure” and the “Nominal Ocular Hazard Distance”.
As the name implies, the MPE is the maximum safe exposure that is allowed, for a given time span. For example, the MPE for a 1/4 second exposure to visible light is 2.5 milliwatts/cm2.
The NOHD is simply where a laser’s beam falls below the MPE. It depends on the laser’s power and beam divergence. The NOHD is the distance from the laser at which the direct beam is not expected to cause any injury or adverse change to the eye.What Williamson and McLin did was extend the MPE and NOHD concepts to dazzle. This is how they came up with the “Maximum Dazzle Exposure” and the “Nominal Ocular Dazzle Distance” discussed below.
Dazzle Level
After an extensive series of tests and scientific papers, Williamson and McLin developed the concepts “Dazzle Level,” “Maximum Dazzle Exposure,” and “Nominal Ocular Dazzle Distance.”
First, the researchers determined that dazzle can be measured in how many degrees of vision that are blocked. They picked four “Dazzle Levels” as significant:
First, the researchers determined that dazzle can be measured in how many degrees of vision that are blocked. They picked four “Dazzle Levels” as significant:




Tech note: When using both eyes, the human field of view is about 200° horizontally and 100° vertically. The photos above are roughly 100° horizontally and 50° vertically. This is done because it is unlikely you would be so close to your computer screen that the above photo would fill your entire vision. So use the above pictures as a guide to the relative sizes of the four Dazzle Levels shown.

The graphics above are from Williamson and McLin’s 2018 paper, showing how they depict the extent of the four dazzle levels, using a 40° field of view. The white areas in the center illustrate light levels so high that the retina is saturated, and the area is perceived without color. The white areas do NOT necessarily indicate whether an afterimage would occur.
[Figure 2, C. A. Williamson and L. N. McLin, “Determination of a laser eye dazzle safety framework”, Journal of Laser Applications 30, 032010 (2018)]
[Figure 2, C. A. Williamson and L. N. McLin, “Determination of a laser eye dazzle safety framework”, Journal of Laser Applications 30, 032010 (2018)]
Try it at home!
You can get an idea of various angle sizes by doing this:
- 2 degrees — Hold your arm straight in front, with your fingers closed and thumb held up. The area blocked by your thumb is roughly 2° (full-angle) in width.
- 10 degrees — Pull in your thumb to make a fist and turn it sideways to block your vision. The area of your fist is roughly 10° in width.
- 20 degrees — Open your hand with fingers and thumb spread. The area covered by your hand (imagine the space between fingers as being filled in) is roughly 20° in width.
- 40 degrees — Put both hands in front you at arms length, with fingers and thumbs spread. Put them so the thumbs touch (“jazz hands”). The area covered by both hands is roughly 40°.
Try it at home!
You can get an idea of various angle sizes by holding your arm and hand out as follows:
- 2 degrees — Hold your arm straight in front, with your fingers closed and thumb held up. The area blocked by your thumb is roughly 2° (full-angle) in width.
- 10 degrees — Pull in your thumb to make a fist and turn it sideways to block your vision. The area of your fist is roughly 10° in width.
- 20 degrees — Open your hand with fingers and thumb spread. The area covered by your hand (imagine the space between fingers as being filled in) is roughly 20° in width.
- 40 degrees — Put both hands in front you at arms length, with fingers and thumbs spread. Put them so the thumbs touch (“jazz hands”). The area covered by both hands is roughly 40° in width.




Measuring angles, when talking about dazzle
Dazzle researchers are concerned with situations where there is light near an object, which is obscuring the object. In talking about this, the angle descriptions can get confusing. Here’s a quick overview.
In the diagram below, a laser beam is going into a person’s eye. The resulting dazzle is obscuring the target. The dazzle can be described as 20° meaning it is obscuring a target that fills 20° of the visual field. Or it can be described as 40° meaning the entire size of the dazzle field.
In the diagram below, a laser beam is going into a person’s eye. The resulting dazzle is obscuring the target. The dazzle can be described as 20° meaning it is obscuring a target that fills 20° of the visual field. Or it can be described as 40° meaning the entire size of the dazzle field.
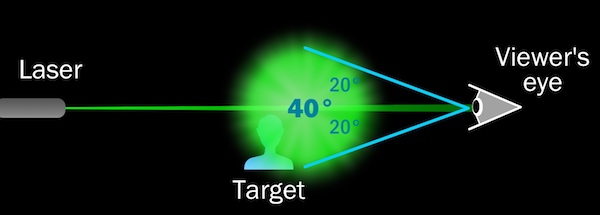
The laser dazzle concept refers to the entire size of the dazzle field — the diameter across, also called the full-angle. In the diagram above, this is the 40° angle. It does not refer to the radius of the dazzle, also called the half-angle (20° in the diagram above).
Also, note that the dazzle angle is NOT the same as the laser beam angle. The light from a narrow laser beam can be scattered inside the eye to create a much larger dazzle field.
Also, note that the dazzle angle is NOT the same as the laser beam angle. The light from a narrow laser beam can be scattered inside the eye to create a much larger dazzle field.
Target size is a factor
Because dazzle can vary so much in angle, Williamson and McLin introduced the concept of a target, meaning “an object to be detected.” For example, the target might be the runway that a pilot needs to see, in order to manually land a plane.
- In the first set of photos above, if the target is simply “the city,” then not even the 40° High dazzle is a problem. Clearly we are over a city!
- But if the target is “the runway,” then any dazzle over about 8° that is centered on the runway is going to block the end of runway and will be a problem. And of course the dazzle field will get larger and larger as the aircraft descends.
Ambient light is a factor
Whether light is dazzling also depends on the ambient light — if it is day, twilight, or dark. The graphics below show how the same amount of light (irradiance) can have very different dazzle effects.

Simulated images giving an approximate representation of human visual dazzle from a green (532 nm) laser from low (0.5 μW·cm-2) to high (500 μW·cm-2) laser irradiances at day (1,000 cd·m-2), dusk/dawn (10 cd·m-2) and night (0.1 cd·m-2) ambient light levels. Each image has a scene horizontal field of view of 40°. [Figure 2, Annex, C. A. Williamson and L. N. McLin, “Determination of a laser eye dazzle safety framework”, Journal of Laser Applications 30, 032010 (2018)]
Laser color is a factor
The human eye is most sensitive to green light. Light of other colors appears less intense. Thus, a green laser will cause more dazzle than a blue or red laser with the same power and divergence. This is shown in the graphics below.

Simulated images showing human dazzle differences between blue (445 nm), green (532 nm) and red (650 nm) lasers of equal irradiance (50 μW·cm-2) at dusk/dawn (10 cd·m-2) conditions. Each image has a scene horizontal field of view of 40°. [Figure 4, Annex, C. A. Williamson and L. N. McLin, “Determination of a laser eye dazzle safety framework”, Journal of Laser Applications 30, 032010 (2018)]
Maximum Dazzle Exposure
The researchers have proposed the following definition of Maximum Dazzle Exposure:
“The MDE is the threshold laser irradiance at the eye below which a given target can be detected. It can also be used as a measure of the minimum laser irradiance required to obscure a given target.”
For laser irradiance levels higher than the MDE, the eye cannot detect the target. For laser irradiance levels lower than the MDE, the eye can detect the target.
They also note “The MDE is applicable for continuous-wave [visible light] laser sources and may also be calculated for the average power of repetitively pulsed laser sources.”
“The MDE is the threshold laser irradiance at the eye below which a given target can be detected. It can also be used as a measure of the minimum laser irradiance required to obscure a given target.”
For laser irradiance levels higher than the MDE, the eye cannot detect the target. For laser irradiance levels lower than the MDE, the eye can detect the target.
They also note “The MDE is applicable for continuous-wave [visible light] laser sources and may also be calculated for the average power of repetitively pulsed laser sources.”
Nominal Ocular Dazzle Distance
Let’s say we’re trying to land an aircraft at night. We are 1,500 feet from a runway. From this distance, the end of the runway takes up 5° (full-angle) of our field of view.
There is someone at one edge of the runway with a laser aimed at us. If the Dazzle Level is Low (10° full-angle), then then entire runway is obscured: the 5° on the runway side, plus 5° on the other side as well.
The concept of Nominal Ocular Dazzle Distance tells us how far the laser beam will go before we can see the 5°-wide runway. We would have to know the laser pointer’s power, beam divergence and wavelength. Note that we also know the target size (5°) and the ambient light (nighttime). Given all these factors, it is possible to calculate the NODD for the pointer.
Here is Williamson and McLin’s definition of NODD:
“The NODD is the minimum distance for the visual detection of a target in the presence of laser dazzle. It also represents the maximum effective range of a laser dazzle system designed to prevent the visual detection of a target.”
The diagram below shows the similarities between the eye hazard levels NOHD (Nominal Ocular Hazard Distance) and MPE (Maximum Permissible Exposure), and the dazzle levels NODD (Nominal Ocular Dazzle Distance) and MDE (Maximum Dazzle Exposure):
There is someone at one edge of the runway with a laser aimed at us. If the Dazzle Level is Low (10° full-angle), then then entire runway is obscured: the 5° on the runway side, plus 5° on the other side as well.
The concept of Nominal Ocular Dazzle Distance tells us how far the laser beam will go before we can see the 5°-wide runway. We would have to know the laser pointer’s power, beam divergence and wavelength. Note that we also know the target size (5°) and the ambient light (nighttime). Given all these factors, it is possible to calculate the NODD for the pointer.
Here is Williamson and McLin’s definition of NODD:
“The NODD is the minimum distance for the visual detection of a target in the presence of laser dazzle. It also represents the maximum effective range of a laser dazzle system designed to prevent the visual detection of a target.”
The diagram below shows the similarities between the eye hazard levels NOHD (Nominal Ocular Hazard Distance) and MPE (Maximum Permissible Exposure), and the dazzle levels NODD (Nominal Ocular Dazzle Distance) and MDE (Maximum Dazzle Exposure):
Example using a 100 mW handheld laser
The information below is from a February 2015 paper on NODD by Williamson and McLin:
“…[T]he laser system being evaluated, representative of a moderately powered handheld laser pointer, can have a laser dazzle effect at significant ranges at nighttime ambient luminance levels.
“A 5° angle of obscuration from the laser axis can be achieved at almost 2 km for a green laser and around 1 km for a red laser of the same 100 mW power level.
“Larger 20° angles of obscuration are possible out to around 0.5 km for green and 0.25 km for red.
“At dawn/dusk light levels, these effective ranges are approximately 10 times less, whereas at daytime light levels, even the smallest 1° obscuration can only be achieved at 0.37 km for green and 0.19 km for red.
“Five degree (red only), and 10° and 20° (both red and green) obscuration extents are not achievable during the day without the laser being closer than the NOHD.”
“A 5° angle of obscuration from the laser axis can be achieved at almost 2 km for a green laser and around 1 km for a red laser of the same 100 mW power level.
“Larger 20° angles of obscuration are possible out to around 0.5 km for green and 0.25 km for red.
“At dawn/dusk light levels, these effective ranges are approximately 10 times less, whereas at daytime light levels, even the smallest 1° obscuration can only be achieved at 0.37 km for green and 0.19 km for red.
“Five degree (red only), and 10° and 20° (both red and green) obscuration extents are not achievable during the day without the laser being closer than the NOHD.”
Factors that influence the Maximum Dazzle Exposure
For visible light, the Maximum Permissible Exposure depends on the laser’s irradiance (power over an area) for a specified time such as 1/4 second. The color of the laser light is not a factor.
In contrast, determining a Maximum Dazzle Exposure requires analysis of many more factors. A complete analysis includes (in rough order of importance):
In contrast, determining a Maximum Dazzle Exposure requires analysis of many more factors. A complete analysis includes (in rough order of importance):
- Ambient light — How bright is the background against which the laser is seen?
- Laser divergence — How much does the beam spread?
- Obscuration extent — How wide does the obscuring light need to be, relative to the target?
- Laser power — A more powerful laser will of course have more dazzling effect
- Laser wavelength — The eye sees greens and yellows better than an equivalent amount of blue or red light
- Target size — How large is the target itself?
- Atmospheric visibility — For long distances of miles or kilometers, how clear is the air?
- Target contrast — Does the target stand out or blend into its background?
- Age of the viewer — In general older persons’ eyes scatter light more, creating more dazzle
- Eye pigmentation — Although this effect is small, whether an eye has a light colored or dark colored iris can make a difference in being dazzled.
Table of MDE limits
Williamson and McLin developed a complex formula for calculating MDE based on the above factors:
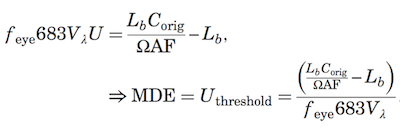
This formula makes sense to laser safety experts — but not necessarily to non-experts who may need more general guidance.
Therefore, in a 2017 presentation the researchers proposed the following table of MDE limits as a general rule (for average ages, targets, eye pigment, etc.).
Therefore, in a 2017 presentation the researchers proposed the following table of MDE limits as a general rule (for average ages, targets, eye pigment, etc.).
Maximum Dazzle Exposure (MDE) in microwatts/cm2
Dazzle Level
Night
Dusk
Day
Very Low (2°)
0.001
0.6
40
Low (10°)
0.04
30
2,000*
Medium (20°)
0.16
120
8,000*
High (40°)
0.6
450
30,000*
Night
Dusk
Day
V. Low 2°
0.001
0.6
40
Low 10°
0.04
30
2,000*
Med. 20°
0.16
120
8,000*
High 40°
0.6
450
30,000*
*This value is above the Maximum Permissible Exposure for the laser. Therefore the MPE would be the maximum irradiance permitted; you would NOT allow exposure to these Maximum Dazzle Exposure values.
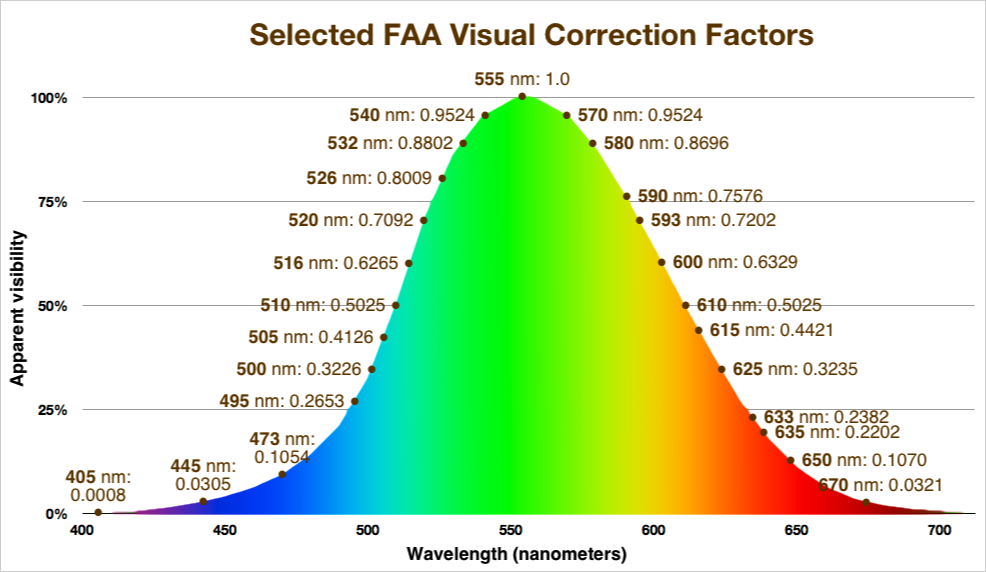
Adjusting for wavelength
The above MDEs are for green light at 555 nanometers This appears brightest to the human eye. To determine visibility for another color (wavelength), divide the value in the table above by the Visual Correction Factor found in the chart below.
The above MDEs are for green light at 555 nanometers This appears brightest to the human eye. To determine visibility for another color (wavelength), divide the value in the table above by the Visual Correction Factor found in the chart below.
For example, if your laser is a 445 nm blue pointer, the VCF is 0.0305. (This is pretty low. The 445 nm blue is only about 3% as visible as green light.)
To find the Low dazzle level at night for a 445 nm laser you would divide the MDE value from the table (0.04) by the VCF of 0.0305. The result is a MDE of 1.3. This means there can be a higher irradiance — 33 times higher in fact — before dazzle from a blue 445 nm laser obscures a 10° (full-angle) target at night, compared with using green light of 555 nm.
To find the Low dazzle level at night for a 445 nm laser you would divide the MDE value from the table (0.04) by the VCF of 0.0305. The result is a MDE of 1.3. This means there can be a higher irradiance — 33 times higher in fact — before dazzle from a blue 445 nm laser obscures a 10° (full-angle) target at night, compared with using green light of 555 nm.
Calculating the NODD
Knowing the MDE for a given scenario (example: nighttime with a Low dazzle level), you can calculate the NODD by the following formula:

Notice that this differs from the similar NOHD equation presented here, in the following ways:
Finally, π of course is 3.14159
- The laser power is in watts, not milliwatts. (5 mW = 0.005 W, 50 mW = 0.05 W, 500 mW = 0.5 W)
- The result is in kilometers; this website normally uses feet. To convert kilometers to feet, divide the kilometers by 0.0003048.
Finally, π of course is 3.14159
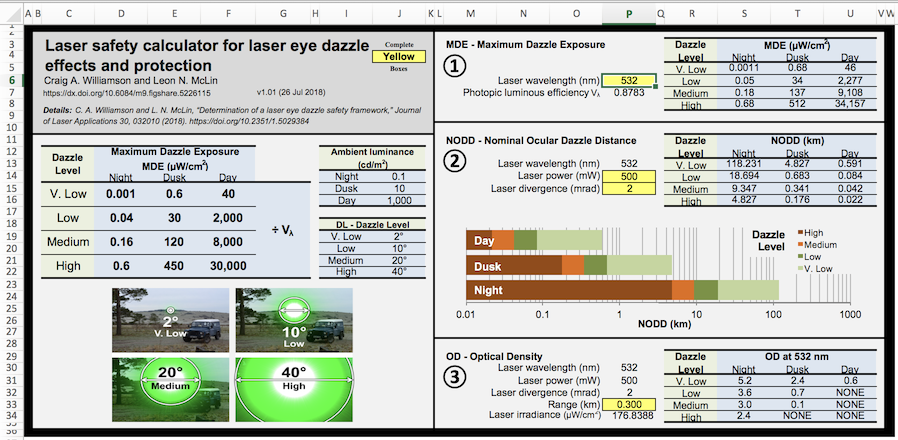
Excel spreadsheet calculator
Williamson and McLin developed an Excel spreadsheet that can be used to calculate the MDE, NODD and the desired Optical Density of eyewear to protect against laser light.
How to use it: Download the Laser safety calculator spreadsheet, and open in Excel. It will open on the “Overview” worksheet. Switch to the “Calculator” worksheet shown below. Enter your data in the four yellow boxes on the right. The numbers in the blue boxes on the right will change, to show the MDE, NODD and OD for the four different Dazzle Levels.
The area on the left does not change. The MDE limits listed are for the brightest possible (highest luminous efficiency) wavelength of 555 nm. The two smaller tables on the left give the light levels used for Night, Dusk and Day, and the angles used for the four Dazzle Levels.
How to use it: Download the Laser safety calculator spreadsheet, and open in Excel. It will open on the “Overview” worksheet. Switch to the “Calculator” worksheet shown below. Enter your data in the four yellow boxes on the right. The numbers in the blue boxes on the right will change, to show the MDE, NODD and OD for the four different Dazzle Levels.
The area on the left does not change. The MDE limits listed are for the brightest possible (highest luminous efficiency) wavelength of 555 nm. The two smaller tables on the left give the light levels used for Night, Dusk and Day, and the angles used for the four Dazzle Levels.
Application to laser/aviation incidents
You might ask “How does this apply to the thousands of laser/aircraft illumination incidents that occur each year?”
The MDE/NODD concept can help estimate the power of the laser that was used in an incident. If the distance to the laser and the size (angle) of the dazzle field can be estimated, and the color is known, this can give an estimate of the laser’s power.
Equations generated by Williamson and McLin can help determine the Optical Density (OD) of laser glare eyewear. This can be useful for police, rescue and other first responder pilots. By knowing the MPE desired to protect against, and the laser irradiance expected to be encountered at a given range, the OD can be calculated. (See the 2015 paper for the equation and details.)
There are some situations where laser light is deliberately aimed at pilots; for example, to warn them away from a restricted area. The MDE/NODD concept allows more accurate determination of the appropriate levels to warn pilots, without unsafely restricting their view.
Based on the researchers’ work, the U.S. FAA or other agencies could possibly revise the afterimage, glare and distraction levels that they currently use to evaluate authorized uses of laser light in airspace. For example, “glare” is currently set at 5 microwatts/cm2 under FAA regulations. However, as the table above indicates, at night a pilot could have a High dazzle level (40°) from just 0.6 microwatts/cm2. It may be that the FAA limits are an order of magnitude too high. In other words, it could be that the FAA is allowing too-high levels of glare.
Important note: Simply aiming a laser beam at an aircraft is illegal in the U.S. and many other countries. It does not matter if a person has done an analysis to find out, for example, that their laser has a NODD of only 100 feet for a Low dazzle level. The aiming is still illegal.
The MDE/NODD concept can help estimate the power of the laser that was used in an incident. If the distance to the laser and the size (angle) of the dazzle field can be estimated, and the color is known, this can give an estimate of the laser’s power.
Equations generated by Williamson and McLin can help determine the Optical Density (OD) of laser glare eyewear. This can be useful for police, rescue and other first responder pilots. By knowing the MPE desired to protect against, and the laser irradiance expected to be encountered at a given range, the OD can be calculated. (See the 2015 paper for the equation and details.)
There are some situations where laser light is deliberately aimed at pilots; for example, to warn them away from a restricted area. The MDE/NODD concept allows more accurate determination of the appropriate levels to warn pilots, without unsafely restricting their view.
Based on the researchers’ work, the U.S. FAA or other agencies could possibly revise the afterimage, glare and distraction levels that they currently use to evaluate authorized uses of laser light in airspace. For example, “glare” is currently set at 5 microwatts/cm2 under FAA regulations. However, as the table above indicates, at night a pilot could have a High dazzle level (40°) from just 0.6 microwatts/cm2. It may be that the FAA limits are an order of magnitude too high. In other words, it could be that the FAA is allowing too-high levels of glare.
Important note: Simply aiming a laser beam at an aircraft is illegal in the U.S. and many other countries. It does not matter if a person has done an analysis to find out, for example, that their laser has a NODD of only 100 feet for a Low dazzle level. The aiming is still illegal.
Sources
Drs. Williamson and McLin have a website, LaserEyeDazzle.com, which has links to various papers and datasets including most of those below.
Craig A. Williamson and Leon N. McLin, “Determination of a laser eye dazzle safety framework”, Journal of Laser Applications 30, 032010 (2018), published online July 18 2018. Available online here. Be sure to click on the Supplemental tab, for a link to the Annex which sets forth a proposed laser eye dazzle safety framework. All content covered by the U.K. Open Government Licence.
Excel MDE/NODD/OD spreadsheet calculator is here. Note that the actual calculator is on sheet 2, and that the user enters data in the yellow cells.
Some information is based on an unpublished paper presented March 23 2017 at the International Laser Safety Conference in Atlanta, Georgia. Thanks to Dr. Williamson for providing PDFs of the presentation slides.
Craig A. Williamson and Leon N. McLin, "Nominal ocular dazzle distance (NODD)," Appl. Opt. 54, 1564-1572 (2015). Available online here.
Craig A. Williamson, J. Michael Rickman, David A. Freeman, Michael A. Manka, and Leon N. McLin, "Measuring the contribution of atmospheric scatter to laser eye dazzle," Appl. Opt. 54, 7567-7574 (2015)
João M. P. Coelho, José Freitas, and Craig A. Williamson, "Optical eye simulator for laser dazzle events," Appl. Opt. 55, 2240-2251 (2016). Using MATLAB and ZEMAX to make a computer model of the eye, using ray tracing and scattering models.
There is a summary of ten days of field trials using a cable car here.
Craig A. Williamson and Leon N. McLin, “Determination of a laser eye dazzle safety framework”, Journal of Laser Applications 30, 032010 (2018), published online July 18 2018. Available online here. Be sure to click on the Supplemental tab, for a link to the Annex which sets forth a proposed laser eye dazzle safety framework. All content covered by the U.K. Open Government Licence.
Excel MDE/NODD/OD spreadsheet calculator is here. Note that the actual calculator is on sheet 2, and that the user enters data in the yellow cells.
Some information is based on an unpublished paper presented March 23 2017 at the International Laser Safety Conference in Atlanta, Georgia. Thanks to Dr. Williamson for providing PDFs of the presentation slides.
Craig A. Williamson and Leon N. McLin, "Nominal ocular dazzle distance (NODD)," Appl. Opt. 54, 1564-1572 (2015). Available online here.
Craig A. Williamson, J. Michael Rickman, David A. Freeman, Michael A. Manka, and Leon N. McLin, "Measuring the contribution of atmospheric scatter to laser eye dazzle," Appl. Opt. 54, 7567-7574 (2015)
João M. P. Coelho, José Freitas, and Craig A. Williamson, "Optical eye simulator for laser dazzle events," Appl. Opt. 55, 2240-2251 (2016). Using MATLAB and ZEMAX to make a computer model of the eye, using ray tracing and scattering models.
There is a summary of ten days of field trials using a cable car here.